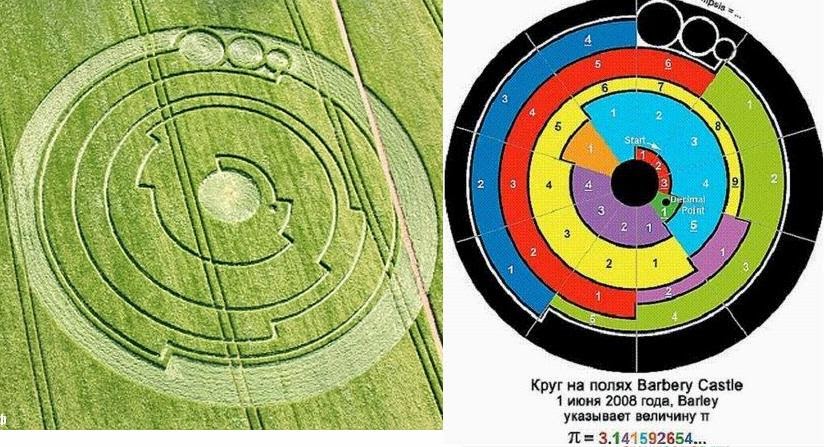
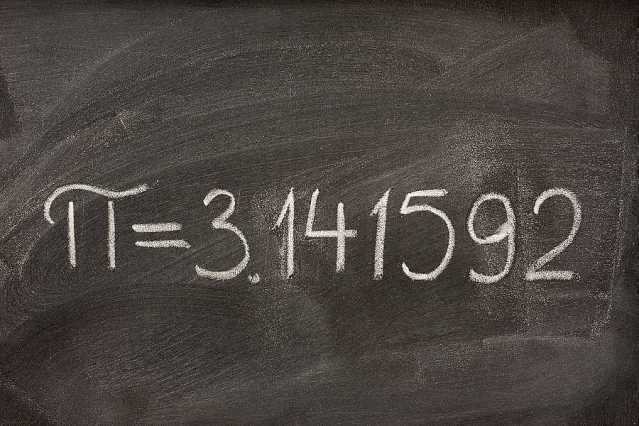Число Пи. В чем уникальность числа Пи и необычные факты о числе Пи.
Число Пи (обозначается как π) – математическая величина, являющаяся постоянным значением: отношением длины окружности к ее диаметру. Сейчас этот параметр используется во многих отраслях математики и физики: редко можно встретить формулу, в которой нет π. В чем уникальность этого числа и какова его история появления?
Краткая история вычислений π
Ученые древнего Междуречья заметили, что длина окружности относится к ее диаметру как постоянная величина. Проводя простейшие расчеты, они пришли к выводу, что число π примерно равно 3.
В древнем Египте широко известен документ писца Армеса, который предположил, что площадь круга с радиусом r эквивалентна площади квадрата с длиной ребра 8/9 * 2r (8/9 относительно диаметра окружности).
Так как площадь круга S = πr2, получаем:
πr2 = (8/9*2r)2 = (16/9)2 * r2 = 256/81r2
По этим расчетам число π получалось равным 3,16.
Максимально точно к современному числовому определению π в древности приблизился Архимед. Он анализировал отношения вписанного и описанного 96-угольника в окружность к ее длине и пришел к неравенству вида:
3 (10/71) < π < 3 (1/7)
Значение π получалось равным 22/7.
До середины 17 столетия ученые продолжали предпринимать попытки нахождения точного определения числа π, постоянно увеличивая количество ребер многоугольников. Математик из Голландии Лудольф ван Цейлен потратил на расчеты 10 лет, в результате чего он получил результат с 20 символами после запятой.
Точное аналитическое выражение числа π первым получил Франсуа Виет. Он установил, что площадь круга с диаметром 1 вычисляется по формуле:
S = "1/2√(1/2) * √(1/2+1/2√(1/2)) * √(1/2+1/2√((1/2)+1/2√(1/2)))…"
Известно, что площадь такого круга равна π/4. Преобразовав выражение, ученый установил:
π/2 = 2/√2*2/√(2+√2) * 2/(√((2)+(√((2)+√(2)))))…
Виет вычислил π с 9 корректными символами после запятой.
Ученый из Англии Джон Мэчин в 1706 году вывел значение числа π со 100 символами после запятой. Он воспользовался формулой Лейбница и переписал ее в виде:
π/4 = 4 arctg(1/5) – arctg(1/239)
Полученный сходящийся ряд позволил рассчитать значение π с высокой точностью.
С появлением компьютерных вычислений появилась возможность получать точные значения числа π с сотнями символов после запятой. Математик из Индии Сриниваса Рамануджан выполнил разложение арктангенса в ряд Тейлора и получил значение π с 600 цифрами.
В 1987 году благодаря расчетам на компьютере братья Чудновские вывели число π с миллионом символов после запятой. В 2009 году ученые из Японии рассчитали на суперкомпьютере π с 2,5 миллионами знаков. В этом же году программист из Франции Фабрису Беллару получил 2 699 999 990 000 символов после запятой, используя обычный компьютер с системой Linux. Его расчеты длились 131 день.
Последний рекорд принадлежит Сингеру Кондо и Александру Йи. Ученые определили значение π с 12,1 триллионами символов после запятой.
Необычные факты о числе π
Существует легенда, что число π использовали в расчетах при постройке Вавилонской башни и храма Соломона. Но неправильные математические вычисления привели к разрушению зданий.
Значение π хотели узаконить на уровне государства. В штате Индиана в 1897 году был подготовлен билль, согласно которому значение π равнялось 3,2. Благодаря своевременному вмешательству нескольких ученых такую ошибку удалось предотвратить.
Шесть девяток, встречающиеся в бесконечном значении числа π носят имя физика из США Ричарда Фейнмана, который изъявил желание выучить все предшествующие им цифры.
Создан специальный клуб последователей числа π. Чтобы вступить в него, нужно выучить как можно больше символов после запятой. Члены клуба полагают, что в значении π находится истина существования Вселенной и смысл бытия.
Разрабатываются механизмы запоминания числа π. Члены клуба придумали принцип запоминания, основанный на соответствии каждой цифры, входящей в π, слову из такого же количества букв. Участники сообщества сочиняют стихи, придуманные согласно этому принципу. Однажды даже был опубликован целый рассказ, включающий 3834 слова, количество букв в которых равнялось цифрам в π.
Люди соревнуются в запоминании символов в π и ставят рекорды. Японец Акира Харагучи выучил более 83000 знаков после запятой числа π. В России максимальный рекорд составляет 2500 знаков и принадлежит жителю Челябинска.
14 марта отмечается день числа π. Физик Ларри Шоу заметил, что написание этой даты (в американской версии – 3.14) аналогично первым трем цифрами числа π.
Особенно этот праздник любим математиками и иными специалистами точных наук. Они расслабляются и веселятся в этот день, а кондитеры выпекают различные изделия в форме π.
14 марта родился создатель теории относительности, физик Альберт Эйнштейн.
В Сиэттле рядом со зданием Музея искусств установили памятник числу π.
Применение числа π
Величина π сейчас используется в самых различных областях современной науки. Это не только отношение длины окружности к ее диаметру, неевклидова геометрия не обходится без π. Эйлер вывел формулу, описывающую связь между π и e:
ei*π + 1 = 0.
С применением числа π можно вычислить любую другую константу, например, постоянную тонкой структуры, постоянную золотой пропорции. Область использования π широка:
- Геометрия.
- Ядерная физика.
- Теория относительности.
- Физика космоса.
- Квантовая механика.
Ученые выяснили, что в расшифрованном ДНК человека число π определяет структуру макромолекулы. Это произвело фурор. Руководитель исследования, доктор Чарльз Кэнтор, отметил: «Это феноменально, число π встречается повсюду, и при этом является неизменной величиной».
Формулы с числом π
Существует много формул для вычисления числа π.
Формула Валлиса:
2/1 * 2/3 * 4/3 * 4/5 * 6/5 * 6/7 * 8/7 * 8/9… = π/2
Она активно используется в теоретических расчетах, поскольку такое медленно сходящееся произведение непригодно для практического применения. С помощью формулы Валлиса получают тождество Стирлинга.
Ряд Лейбница:
1/1 – 1/3 + 1/5 – 1/7 + 1/9… = π/4
Это выражение используется в вычислениях математического анализа.
Другие вычисления с помощью рядов:
1/2∑1/16k (8/(8k+2) + 4/(8k+3) + 4/(8k+4) – 1/(8k+7)) = 1/4∑1/16k (8/(8k+1) + 8/(8k+2) +4/(8k+3) – 2/(8k+5) – 2/(8k+6) – 1/(8k+7)) = ∑(-1)k/4k (2/(4k+1) + 2/(4k+2) + 1/(4k+3)) = π, где суммирование ведется при значениях k от нуля до бесконечности.
π = 2√3∑(-1)k/(3k(2k+1))
Вычисления с помощью пределов:
π = lim(((m!)424m)/[(2m)!]2m)
π = lim (2n * √(2 - √(2 + √(2 + √(2…√2)))))
m и n стремятся к бесконечности.
n равно количеству корней в формуле.
Вычисления с помощью пределов являются основными расчетами в высшей математике.
Интеграл Пуассона:
√ π = ∫e-x2dx, где интеграл считается от -∞ до +∞.
Эта формула подходит для решения краевой задачи и уравнений с частными производными.
Интегральный синус:
∫(sin x/x)dx = π, где интеграл считается от -∞ до +∞.
Формула применяется для решения специальных тригонометрических уравнений в высшей математике.
Несобственный интеграл:
∫dx/((x+1)√x) = π, где интеграл считается от 0 до +∞.
Несобственные интегралы используются при расчетах площадей бесконечно длинных и бесконечно высоких криволинейных трапеций.
Возможности, которые дает математикам число π, безграничны. В перспективе это бесконечное число может содержать всю информацию, находящуюся во Вселенной. Изучение числа π продолжается учеными до сих пор.
Читать дальше:
Что мы знаем о числах-гигантах. Примеры чисел-гигантов из окружающего мира. Большие числа славян и древних римлян.

Перевод из двоичной системы счисления в десятичную. Сложение, вычитание, умножение, деление в двоичной системе счисления.
Тригонометрическая форма записи комплексного числа. Действия над комплексными числами: сложение, вычитание, умножение, деление.